Υπολογισμοί πυκνωτή επαγωγέα

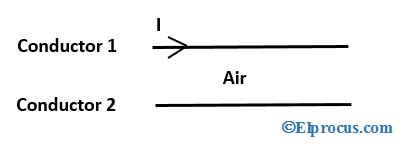
Οι επαγωγείς μπορούν να φανταστούν το αντίθετο των πυκνωτών. Η κύρια διαφορά μεταξύ ενός πυκνωτή και ενός επαγωγέα είναι ότι ένας πυκνωτής μεταφέρει ένα προστατευτικό διηλεκτρικό μεταξύ των πλακών του, το οποίο αναστέλλει την αγωγή του ρεύματος στα άκρα του. Εδώ λειτουργεί σαν ανοιχτό κύκλωμα.

Από την άλλη πλευρά, η επαγωγή ενός επαγωγέα είναι συνήθως (αν και όχι πάντα) εξαιρετικά χαμηλής ή ελάχιστης αντίστασης. Συμπεριφέρεται ουσιαστικά σαν κλειστό κύκλωμα.

Πυκνωτής επαγωγικότητα δυαδικότητας

Υπάρχει ένας μοναδικός όρος στα ηλεκτρονικά για αυτόν τον τύπο σχέσης μεταξύ δύο παραμέτρων ενός κυκλώματος ή τμημάτων ενός κυκλώματος. Τα στοιχεία αυτού του τύπου ζευγαριού είναι γνωστά ως διπλά το ένα με το άλλο . Για παράδειγμα, ανάλογα με την ικανότητα αγωγής ρεύματος, ένα ανοικτό κύκλωμα είναι το διπλό κλειστό κύκλωμα.

Στην ίδια αρχή, ένας επαγωγέας είναι το διπλό του πυκνωτή. Η δυαδικότητα των επαγωγέων και των πυκνωτών είναι πολύ βαθύτερη από τη φυσική ικανότητα να ρέει ρεύμα.

Σε αυτό το άρθρο, συγκρίνουμε την αρχή λειτουργίας του πηνίου και του πυκνωτή και αξιολογούμε τα αποτελέσματα με υπολογισμούς και τύπους.

Παρά το γεγονός ότι οι επαγωγείς συνήθως φαίνονται σπάνια σε ηλεκτρονικά κυκλώματα, δεδομένου ότι σήμερα αντικαθίσταται κυρίως από opamps σε ενεργά φίλτρα), τα άλλα μέρη που εμπλέκονται σε ένα κύκλωμα φαίνεται να έχουν κάποια ποσότητα επαγωγής.

Η αυτοδιέγερση των ακροδεκτών ενός πυκνωτή ή αντίστασης γίνεται ένα μεγάλο ζήτημα σε κυκλώματα υψηλής συχνότητας, κάτι που εξηγεί γιατί οι αντιστάσεις και οι πυκνωτές στερέωσης επιφανείας χωρίς μόλυβδο χρησιμοποιούνται τόσο συχνά σε τέτοιες εφαρμογές.

Βασικές εξισώσεις πυκνωτών

Η θεμελιώδης εξίσωση για τους πυκνωτές είναι αυτή με την οποία ορίζεται το farad:

C = Q / I [Εξ. 19]

όπου το C είναι η χωρητικότητα στο farad, το Q είναι το φορτίο στο coulomb και το U είναι το pd μεταξύ των πλακών σε volt.

Μέσω Εξ. 19, λαμβάνουμε έναν τύπο της φόρμας Q = ∫ I dt + c όπου c είναι η αρχική χρέωση, εάν υπάρχει. Έχοντας αναγνωρίσει το Q, μπορούμε να προσδιορίσουμε το U από την Εξ. 19:

U = 1 / C ∫ I dt + c / C [Εξ. 21]

Ένα σημαντικό χαρακτηριστικό ενός πυκνωτή μπορεί να είναι έτσι, εάν εφαρμόζεται περιοδικό ρεύμα σε αυτό (συνήθως ένα ρεύμα που ταλαντεύεται ημιτονοειδώς), το φορτίο στον πυκνωτή και η τάση που διασχίζει επίσης κυμαίνονται ημιτονοειδώς.

Η καμπύλη φόρτισης ή τάσης είναι μια αρνητική καμπύλη συνημίτονο ή μπορούμε να την φανταστούμε ως ημιτονοειδής καμπύλη που υστερεί από την τρέχουσα καμπύλη κατά π / 2 λειτουργία (90 °).

Η θεμελιώδης εξίσωση που καθορίζει το henry, τη μονάδα αυτεπαγωγής, είναι

L = ΝΦ / Ι [Εξ. 22]

Με αναφορά σε ένα μόνο πηνίο, η αυτοαγωγιμότητα στο henry μπορεί να είναι η σχέση fl ux (το μαγνητικό flx<1) in weber multiplied by the number of winding N, (because the magnetic flux cuts through each turn), when a unit current passes through it (I = 1 A). An even more handy definition could be extracted from Eq. 22, using Neumann’s equation. This claims that:

U = N (dΦ / dt) [Εξ. 23]

Αυτό που προτείνει αυτή η εξίσωση είναι το γεγονός ότι το e.m.f. που προκαλείται μέσα σε έναν επαγωγέα σχετίζεται με τον συνδεδεμένο ρυθμό μεταβολής της ροής.

Όσο πιο γρήγορη η διακύμανση της ροής, τόσο υψηλότερη είναι η επαγόμενη e.m.f. Για παράδειγμα, όταν η ροή πάνω από τον πηνίο ή το πηνίο αυξάνεται με ρυθμό 2 mWb s^-1, και υποθέτοντας ότι το πηνίο έχει ΔΕΥΤΕΡΟ ΠΕΝΤΕ στροφές, τότε U = 25x2 = 50V.

Η διαδρομή του e.m.f. είναι τέτοια ώστε να αντιστέκεται στις μεταβολές της ροής, όπως περιγράφονται από τον νόμο του Lenz.

Αυτή η αλήθεια επισημαίνεται πολλές φορές προηγουμένως της δεξιάς πλευράς της εξίσωσης με ένα σύμβολο μείον, ωστόσο, αρκεί να πιστεύουμε ότι το U είναι το πίσω e.m.f., το σημείο θα μπορούσε να αφαιρεθεί.

Διαφορές

Ο όρος dΦ / dt σε Εξ. Το 23 δείχνει τι μάθαμε ως το ρυθμό μεταβολής του x ux. Η φράση ονομάζεται η διαφορά του Φ σε σχέση με το t και ένας ολόκληρος κλάδος αριθμητικής είναι αφιερωμένος στην εργασία με τέτοιου είδους εκφράσεις. Η φράση έχει τη μορφή ενός μοναδικού αριθμού (dΦ) διαιρούμενο με μία ακόμη ποσότητα (dt)

Οι διαφορές χρησιμοποιούνται για να συσχετίσουν πολλά σύνολα αναλογιών: dy / dx, για παράδειγμα, συσχετίζει τις μεταβλητές x και y. Όταν ένα γράφημα απεικονίζεται χρησιμοποιώντας τιμές x κατά μήκος του οριζόντιου άξονα και τιμές y κατά τον κατακόρυφο άξονα, το dy / dx υποδηλώνει πόσο απότομη είναι η κλίση ή κλίση του γραφήματος.

Εάν το U είναι η τάση πηγής πύλης FET, όπου το Τ είναι το σχετικό ρεύμα αποστράγγισης, τότε το dI / dU δηλώνει την ποσότητα με την οποία αλλάζω για δεδομένες αλλαγές στο U. Εναλλακτικά μπορούμε να πούμε ότι το dI / dU είναι η trans-αγωγιμότητα. Ενώ συζητάμε για επαγωγείς, το dΦ / dt θα μπορούσε να είναι ο ρυθμός αλλαγής της ροής με το χρόνο.

Ο υπολογισμός μιας διαφοράς μπορεί να θεωρηθεί ως η αντίστροφη διαδικασία ολοκλήρωσης. Δεν υπάρχει επαρκής χώρος σε αυτό το άρθρο για να εξετάσει τη θεωρία της διαφοροποίησης, ωστόσο θα καθορίσουμε έναν πίνακα με τις κοινώς χρησιμοποιούμενες ποσότητες μαζί με τις διαφορές τους.

Τυπικές διαφορές

Ο παραπάνω πίνακας λειτουργεί χρησιμοποιώντας τους I και t ως παράγοντες αντί για τη ρουτίνα x και y. Έτσι ώστε οι λεπτομέρειες του να αφορούν συγκεκριμένα τα ηλεκτρονικά.

Για παράδειγμα, λαμβάνοντας υπόψη ότι I = 3t +2, ο τρόπος που αποκλίνω σε σχέση με το χρόνο μπορεί να απεικονιστεί στο γράφημα του Σχ. 38. Για να βρείτε τον ρυθμό μεταβολής του I ανά πάσα στιγμή, εκτιμούμε dI / dt, κατά αναφερόμενος στον πίνακα.

Το πρώτο στοιχείο στη συνάρτηση είναι 3t ή, για να το μορφοποιήσετε ως την πρώτη γραμμή του πίνακα, 3t¹. Ifn = 1, η διαφορά είναι 3t^1-1= 3 τόνους⁰.

Από τ⁰= 1, η διαφορά είναι 3.

Η δεύτερη ποσότητα είναι 2, που μπορεί να εκφραστεί ως 2t⁰.

Αυτό αλλάζει n = 0 και το μέγεθος της διαφοράς είναι μηδέν. Η διαφορά μιας σταθεράς θα είναι πάντα μηδέν. Συνδυάζοντας και τα δύο, έχουμε:

dI / dt = 3

Σε αυτήν την απεικόνιση το διαφορικό δεν περιλαμβάνει t, αυτό σημαίνει ότι η διαφορά δεν εξαρτάται από το χρόνο.

Με απλά λόγια, η κλίση ή η κλίση της καμπύλης στο Σχ. 38 είναι 3 συνεχώς συνεχώς. Το σχήμα 39 παρακάτω δείχνει την καμπύλη για διαφορετική συνάρτηση, I = 4 sin 1.5t.

Με αναφορά στον πίνακα, α = 1,5 και b = 0 σε αυτήν τη συνάρτηση. Ο πίνακας δείχνει, dl / dt = 4x1.5cos1,5t = 6cos 1,5t.

Αυτό μας ενημερώνει για το στιγμιαίο ρυθμό αλλαγής του I. Για παράδειγμα, σε t = 0,4, dI / dt = 6cos0,6 = 4,95. Αυτό θα μπορούσε να παρατηρηθεί στο Σχ. 39, όπου η καμπύλη για 6 cos0.6t περιλαμβάνει την τιμή 4,95 όταν t = 0,4.

Μπορούμε επίσης να παρατηρήσουμε ότι η κλίση της καμπύλης 4sin1,5t είναι 4,95 όταν t = 0,4, όπως φαίνεται από την εφαπτομένη στην καμπύλη σε αυτό το σημείο, (σε σχέση με τις διαφορετικές κλίμακες στους δύο άξονες).

Όταν t = π / 3, ένα σημείο όταν το ρεύμα είναι στο υψηλότερο και σταθερό του, στην περίπτωση αυτή dI / dt = 6cos (1,5xπ / 3): 0, που αντιστοιχεί σε μηδενική μεταβολή του ρεύματος.

Αντίθετα, όταν t = 2π / 3 και το ρεύμα αλλάζουν στο υψηλότερο δυνατό επίπεδο από θετικό σε αρνητικό, dI / dt = 6cosπ = -6, βλέπουμε την υψηλότερη αρνητική τιμή του, παρουσιάζοντας υψηλή μείωση ρεύματος.

Το απλό πλεονέκτημα των διαφορών είναι ότι μας επιτρέπουν να καθορίσουμε ρυθμούς αλλαγής για συναρτήσεις που είναι πολύ πιο περίπλοκες σε σύγκριση με το I = 4sin 1.5t, και χωρίς να χρειάζεται να σχεδιάσουμε τις καμπύλες.

Επιστροφή στους υπολογισμούς

Αναδιοργανώνοντας τους όρους στην Εξ. 22 παίρνουμε:

Φ = (L / N) I [Εξ. 24]

Όπου L και N έχουν σταθερές διαστάσεις, αλλά Φ και I μπορεί να έχει αξία σε σχέση με το χρόνο.

Η διαφοροποίηση των δύο πλευρών της εξίσωσης σε σχέση με το χρόνο δίνει:

dΦ / dt = (L / N) (dI / dt) [Εξ. 25]

Η συγχώνευση αυτής της εξίσωσης με το εξ. 23 δίνει:

U = N (L / N) (dI / dt) = L (dI / dt) [Εξ. 26]

Αυτός είναι ένας άλλος τρόπος έκφρασης του Αυτεπαγωγής . Μπορούμε να πούμε ότι, ένα πηνίο με αυτοαγωγιμότητα 1 Η, αλλαγή ρεύματος 1 Α δευτερόλεπτα^-1δημιουργεί ένα πίσω e.m.f. 1 V. Δεδομένης μιας συνάρτησης που καθορίζει πώς ένα ρεύμα μεταβάλλεται με το χρόνο, Εξ. 26 μας βοηθά υπολογίστε το πίσω e.m.f. ενός επαγωγέα ανά πάσα στιγμή.

Ακολουθούν μερικά παραδείγματα.

A) I = 3 (σταθερό ρεύμα 3 A) dl / dt = 0. Δεν μπορείτε να βρείτε καμία αλλαγή ρεύματος, επομένως το πίσω e.m.f. είναι μηδέν.

B) I = 2t (ρεύμα ράμπας) dI / dt = 2 A s^-1. Με ένα πηνίο που φέρει L = 0,25 H, το πίσω e.m.f. θα είναι σταθερή στα 0,25x2 = 0,5 V.

C) I = 4sin1,5t (το ημιτονοειδές ρεύμα που δόθηκε στην προηγούμενη εικόνα dl / dt = 6cos 1.5t. Δεδομένου ενός πηνίου με L = 0.1 H, το στιγμιαίο πίσω emf είναι 0.6cos1.5t. Το πίσω emf ακολουθεί την καμπύλη διαφορικής του Σχ. 39, αλλά με πλάτος 0,6 V αντί για 6 A.

Κατανόηση των «διπλών»

Οι ακόλουθες δύο εξισώσεις σημαίνουν την εξίσωση ενός πυκνωτή και ενός επαγωγέα αντίστοιχα:

Μας βοηθά να προσδιορίσουμε το επίπεδο της τάσης που παράγεται σε όλη τη συνιστώσα με το ρεύμα να ποικίλει σε χρόνο σύμφωνα με μια συγκεκριμένη λειτουργία.

Ας αξιολογήσουμε το αποτέλεσμα που αποκτήθηκε από το διαφοροποιώντας οι πλευρές L και H του Eq.21 σε σχέση με το χρόνο.

dU / dt = (1 / C) I

Όπως γνωρίζουμε ότι η διαφοροποίηση είναι το αντίστροφο της ολοκλήρωσης, η διαφοροποίηση του ∫It αντιστρέφει την ολοκλήρωση, με μόνο το I ως αποτέλεσμα.

Η διαφοροποίηση του c / C δίνει μηδέν και η αναδιάταξη των όρων παράγει τα εξής:

I = C.dU / dt [Εικ.27]

Αυτό μας επιτρέπει να γνωρίζουμε την κατεύθυνση του ρεύματος είτε πηγαίνει προς τον πυκνωτή είτε βγαίνει από αυτό, σε απόκριση μιας τάσης που ποικίλλει ανάλογα με μια δεδομένη λειτουργία.

Το ενδιαφέρον είναι ότι τα παραπάνω τρέχουσα εξίσωση πυκνωτή μοιάζει με την εξίσωση τάσης (26) ενός επαγωγέα, ο οποίος εμφανίζει το χωρητικότητα, δυαδικότητα επαγωγής.

Ομοίως, η διαφορά ρεύματος και δυναμικού (pd) ή ο ρυθμός μεταβολής ρεύματος και pd μπορεί να είναι διπλά όταν εφαρμόζονται σε πυκνωτές και επαγωγείς.

Τώρα, ας ενσωματώσουμε το Eq.26 σε σχέση με το χρόνο για να ολοκληρώσουμε το quatret εξίσωσης:

∫ U dt + c = LI

Το ακέραιο του dI / dt είναι = I, αναδιατάσσουμε τις εκφράσεις για να λάβουμε:

I = 1 / L∫ U dt + e / L

Αυτό μοιάζει πάλι πολύ παρόμοιο με το Eq.21, αποδεικνύοντας περαιτέρω τη διπλή φύση της χωρητικότητας και της επαγωγής, καθώς και το pd και το ρεύμα τους.

Μέχρι τώρα έχουμε ένα σύνολο τεσσάρων εξισώσεων που μπορούν να χρησιμοποιηθούν για την επίλυση προβλημάτων που σχετίζονται με πυκνωτές και επαγωγείς.

Για παράδειγμα, το Eq.27 μπορεί να εφαρμοστεί για την επίλυση του προβλήματος όπως αυτό:

Πρόβλημα: Ένας παλμός τάσης που εφαρμόζεται σε 100uF παράγει μια καμπύλη όπως φαίνεται στο παρακάτω σχήμα.

Αυτό μπορεί να καθοριστεί χρησιμοποιώντας την παρακάτω συνάρτηση.

Υπολογίστε το ρεύμα που κινείται μέσω του πυκνωτή και σχεδιάστε τα αντίστοιχα γραφήματα.

Λύση:

Για το πρώτο στάδιο εφαρμόζουμε το Eq.27

I = C (dU / dt) = 0

Για τη δεύτερη περίπτωση όπου το U μπορεί να αυξάνεται με σταθερό ρυθμό:

I = C (dU / dt) = 3C = 300μA

Αυτό δείχνει ένα συνεχές ρεύμα φόρτισης.

Για το τρίτο στάδιο όταν το U πέφτει με εκθετικό τρόπο:

Αυτό δείχνει ότι το ρεύμα ρέει μακριά από τον πυκνωτή σε εκθετικό μειωμένο ρυθμό.

Σχέση φάσης

Στην παραπάνω εικόνα, ένα εναλλασσόμενο pd εφαρμόζεται σε έναν επαγωγέα. Αυτό το pd ανά πάσα στιγμή μπορεί να εκφραστεί ως:

Όπου το Uo είναι η μέγιστη τιμή του pd. Αν αναλύσουμε το κύκλωμα με τη μορφή βρόχου και εφαρμόσουμε τον νόμο τάσης του Kirchhoff σε δεξιόστροφη κατεύθυνση, λαμβάνουμε:

Ωστόσο, δεδομένου ότι το ρεύμα είναι ημιτονοειδές εδώ, οι όροι στο βραχίονα πρέπει να έχουν την τιμή ίση με το μέγιστο ρεύμα Io, επομένως έχουμε τελικά:

Αν συγκρίνουμε τα Eq.29 και Eq.30, διαπιστώνουμε ότι το τρέχον I και η τάση U έχουν την ίδια συχνότητα και υστερούμε το U από π/2.

Οι προκύπτουσες καμπύλες μπορούν να είναι μελέτες στο ακόλουθο διάγραμμα:

ντο

Αυτό δείχνει την αντίθετη σχέση μεταξύ πυκνωτή και επαγωγέα. Για ένα ρεύμα επαγωγέα καθυστερεί τη διαφορά δυναμικού κατά π / 2, ενώ για έναν πυκνωτή, το ρεύμα οδηγεί το pd. Αυτό δείχνει πάλι τη διπλή φύση των δύο συστατικών.